|
|
Правило Леонардо
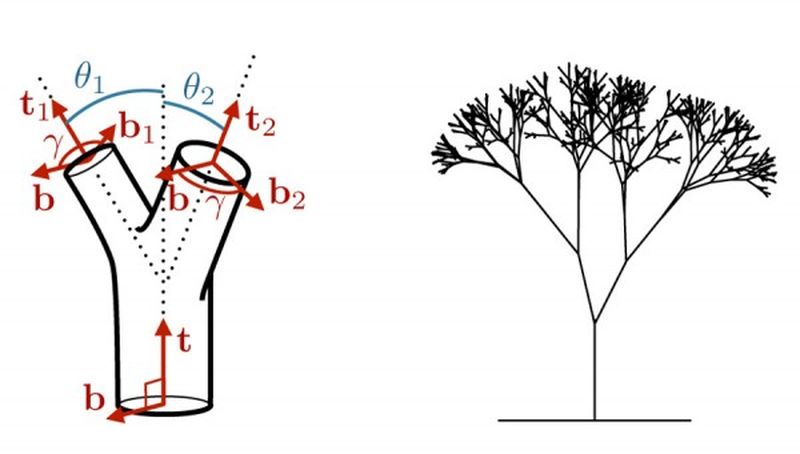
Грациозный ствол дерева разделяется на ветви, сперва немногочисленные и мощные, а те — на все более тонкие. Это так прекрасно и так естественно, что вряд ли кто-нибудь из нас обращал внимание на простую закономерность. Дело в том, что общая толщина ветвей на определенной высоте всегда равна толщине ствола. Этот факт уже 500 лет назад заметил Леонардо Да Винчи, который, как известно, был очень наблюдательным. Взаимосвязь получила название «Правило Леонардо» и долгое время никто не мог понять, почему так происходит. В 2011-м году физик Кристоф Эллой из Калифорнийского университета предложил собственное любопытное объяснение.
«Правило Леонардо» справедливо практически для всех известных видов деревьев. О нем осведомлены и создатели компьютерных игр, создающие реалистичные трехмерные модели деревьев. Более точно, правило это устанавливает, что в месте, где ствол или ветвь раздваивается, сумма сечений раздвоенных веток будет равна сечению исходной ветви. Когда затем и эта ветка раздвоится, сумма сечений уже четырех ее ответвлений будет по-прежнему равна сечению исходного ствола. И так далее.
Еще изящнее это правило записывается математически. Если ствол диаметром D разделяется на произвольное число ветвей n с диаметрами d1, d2 и так далее, сумма их диаметров, возведенных в квадрат, будет равна квадрату диаметра ствола. По формуле: D2 = ∑di2, где i = 1, 2, … n. В реальной жизни степень не всегда строго равна двум и может варьировать в пределах 1,8−2,3, в зависимости от особенностей геометрии того или иного дерева, но в целом зависимость строго соблюдается. До работы Эллоя основной считалась версия о наличии связи между правилом Леонардо и питанием деревьев. Чтобы объяснить этот феномен, ботаники предположили, что подобное отношение оптимально для работы системы трубок, по которым вода поднимается от корней дерева к листве. Идея выглядит вполне обоснованной хотя бы потому, что от квадрата радиуса прямо зависит площадь сечения, определяющая пропускную способность трубы. Однако французский физик Кристоф Элой (Christophe Eloy) с этим не согласен — по его мнению, связана такая закономерность не с водой, а с воздухом. Для обоснования своей версии ученый создал математическую модель, которая связывает площадь листвы дерева с действующей на излом силой ветра. Дерево в ней описывалось, как закрепленное лишь в одной точке (месте условного ухода ствола под землю), и представляющее собой ветвящуюся фрактальную структуру (т.е. такую, в которой каждый меньший элемент представляет собой более или менее точную копию старшего). Добавив к этой модели давление ветра, Эллой ввел определенный постоянный показатель его предельной величины, после которой ветви начинают ломаться. Исходя из этого, он произвел расчеты, которые показали бы оптимальную толщину разветвляющихся веток, такую, при которой сопротивление силе ветра было бы наилучшим. И что же — он пришел ровно к той же зависимости, причем идеальное значение той же величины лежало между 1,8 и 2,3.
Простоту и элегантность идеи и ее доказательства уже оценили специалисты. Так, массачусетский инженер Педро Рейс (Pedro Reis) комментирует: «Исследование ставит деревья на высоту искусственных сооружений, специально просчитанных для сопротивления ветру — лучшим примером которых является Эйфелева башня». Осталось дождаться, что скажут на это ботаники. «В своей работе Эллой использовал простой механический подход. Он рассмотрел дерево как фрактал (фигуру, обладающую некоторой степенью самоподобия), причем каждая ветка моделировалась как балка со свободным концом. В этих предположениях (а также при условии постоянства по времени вероятности слома ветки под воздействием ветра) оказалось, что закон Леонардо минимализирует вероятность того, что ветки дерева сломаются под напором ветра.» Коллеги Эллоя, в целом, согласились с его выкладками и даже заявили, что объяснение довольно простое и очевидное, однако никто до него раньше почему-то не додумался. Что ж, в науке такое — не редкость. 17-11-2015 | Просмотров: 5265
Комментарии
Комментировать
Комментировать
|
Ещё по теме
|
|
|