Математические задачи от профессора Сигма

С 1981 по 1984 год на Всесоюзном радио ежемесячно работал математический радиокружок «Сигма». Аудиозаписи нескольких занятий можно найти в Интернете. Однажды профессор Сигма и его постоянные помощники мальчик Альфа и девочка Бета пришли в гости в журнал «Квант». Мы перепечатываем рассказ об этой встрече.

 

Сигма. Мы начнём с задачи из «Кванта» для младших школьников» (№ 1 за 1981 г.): «В Советском Союзе население составляет 260 млн человек. Казалось бы, на карте СССР с масштабом 1:1 000 000 (в одном сантиметре 10 километров) может поместиться в миллион раз меньше людей, чем на всей территории страны, то есть может поместиться 260 человек. Однако из опыта известно, что и пяти десяткам человек это будет нелегко сделать. Почему?»

 

Альфа. Да я эту задачу сразу решил! Ведь люди живут в многоэтажных домах, значит, на единицу земной поверхности приходится не один, а несколько человек.

 

Сигма. Мы начнём с задачи из «Кванта» для младших школьников» (№ 1 за 1981 г.): «В Советском Союзе население составляет 260 млн человек. Казалось бы, на карте СССР с масштабом 1:1 000 000 (в одном сантиметре 10 километров) может поместиться в миллион раз меньше людей, чем на всей территории страны, то есть может поместиться 260 человек. Однако из опыта известно, что и пяти десяткам человек это будет нелегко сделать. Почему?»

 

Бета. А по-моему, Альфа, ты не прав. Возьмём, например, такое густонаселённое здание, как здание школы. Первого сентября все, кто находятся в этом здании, выходят во двор на линейку, посвящённую началу учебного года. Также и жители других домов могут разместиться во дворах и на улицах — им даже не будет тесно. А ещё остаются степи, пустыни, тундра!

 

Сигма. Бета права. Тебе, Альфа, придётся поискать другое объяснение. А пока попробуй сравнить площади квадратов со сторонами 2 и 1.

 

Альфа. Ну как же — площадь первого будет в четыре раза больше, чем площадь второго. И вообще, при уменьшении размеров любой фигуры в N раз её площадь уменьшается в N² раз. Не зря площадь измеряется в квадратных единицах!

 

Бета. Теперь всё ясно! Человек занимает на Земле определённую часть площади. При изображении на карте с масштабом 1:1 000 000 площади всех фигур уменьшаются в 1 000 000² раз, то есть в 10¹² раз. Именно на это число, а не на миллион и нужно разделить население страны. При этом получится около одной четырёхтысячной части человека, и никакой парадокс не возникает.

А теперь решим ещё одну задачу. В два одинаковых заполненных водой ведра засыпают дробь: в первое ведро крупную, а во второе — мелкую. В каждое ведро насыпают столько дроби, сколько помещается. Из какого ведра выльется больше воды?

 

Сигма. Очень хорошо, ребята, вы во всём разобрались. Мне остаётся лишь добавить, что при решении задачи вы воспользовались так называемыми соображениями подобия. Тема нашего занятия как раз — соображения подобия.

 

Альфа. Ну конечно, из второго, в него насыпают мелкую дробь!

 

Бета. Ну и что?

 

Альфа. Раз дробь мелкая, то и промежутки между отдельными дробинками будут маленькими. Поэтому мелкая дробь уляжется плотнее.

 

 

Бета. Хотя промежутки между крупными дробинками и большие, зато самих промежутков будет меньше. Так что ещё неизвестно, какая дробь уляжется плотнее: мелкая или крупная.

Сигма. Действительно, надо выяснить, какая дробь уляжется плотнее: мелкая или крупная. Давайте для простоты предположим, что отношение диаметров дробинок равно двум. Теперь посмотрим на ведро с мелкой дробью в бинокль с двукратным увеличением. Что мы увидим?

 

Альфа. Мы увидим ведро, заполненное крупной дробью. При двукратном увеличении и объём ведра, и объём каждой дробинки увеличится в 8 раз (8 = 2³), а их отношение останется неизменным. Значит, плотность мелкой и крупной дроби будет одинаковой.

 

Бета. Получается, что из вёдер вытечет одинаковое количество воды. Вот никогда бы не подумала!

 

Сигма. Тем не менее, это правильный ответ. И получить его нам помогли соображения подобия. Хочу только внести небольшое уточнение: наш ответ верен, если размеры дробинок намного меньше размеров ведра. Если же дробинки крупные (или ведро совсем маленькое), то наши рассуждения теряют силу. Причина в том, что мы пренебрегли нарушением правильного расположения дробинок вблизи стенок ведра. А если дробинки большие, то влиянием стенок ведра пренебречь уже нельзя.

 

Бета. Профессор Сигма, а какие ещё задачи можно решать с помощью соображений подобия?

 

Сигма. Соображения подобия оказались очень полезными в биологии. А впервые их применил к изучению строения животных великий итальянский учёный XVI века Галилео Галилей. Его занимал вопрос, как могло бы выглядеть очень крупное сухопутное животное, например гигантская собака. В одной из книг Галилея можно даже найти рисунки костей такой воображаемой собаки.

 

 

Сигма. Нет, всё не так просто. Прочность костей пропорциональна площади их поперечного сечения. При увеличении размеров в 10 раз эта площадь увеличится в 100 (=10²) раз. Значит, кости гигантской собаки смогут выдержать стократную нагрузку. Но в том-то и дело, что нагрузка возрастёт не в 100, а в тысячу раз. Ведь нагрузка пропорциональна массе животного, то есть его объёму. Объём же увеличится в 1000 (=10³) раз. Вот и получается, что гигантская собака не сможет выдержать собственный вес.

 

Альфа. А о чём здесь думать? Увеличить скелет обычной собаки раз в десять — и всё!

 

Бета. Но ведь живут же на Земле очень крупные животные: слоны, носороги...

 

 

Сигма. Да, но ноги у них относительно толще, чем у мелких животных. А вот киты и вовсе не смогли бы жить на суше¹.

Альфа. Я читаю сейчас «Путешествие Гулливера». Гулливер попадает в страну лилипутов, которые в 12 раз меньше него, и в страну великанов, которые больше него тоже в 12 раз. Что же, Джонатан Свифт не учёл того, что было известно уже Галилею?

 

Сигма. Автор «Путешествия Гулливера» старался пользоваться соображениями подобия. Например, описывая обед Гулливера или пошив его костюма. В других местах, однако, Свифт не обошёлся без ошибок — как в истории с яблоком, попавшим в Гулливера в стране великанов.

 

Бета. А я это всё знаю — прочитала в «Кванте» в статье «Из книг Я. И. Перельмана»².

 

Альфа. Профессор Сигма, а почему муравьи могут переносить тяжести во много раз больше собственного веса, а человек не может?

 

Бета. Почему?

 

Сигма. Известно, что сила мышц определяется только площадью их поперечного сечения и не зависит от их длины. Площадь же пропорциональна квадрату линейных размеров, а вес — кубу. Значит, на единицу веса у муравья приходится большая сила, чем у человека и тем более чем у слона. Этим же соотношением между площадью и объёмом объясняется то, что муравьи не могли бы быть теплокровными.

 

Сигма. Количество тепла, вырабатываемого в организме, пропорционально объёму тела. А вот количество тепла, излучаемого в окружающее пространство, пропорционально площади поверхности — ведь теплообмен происходит через кожу. Как мы видели, на единицу объёма у маленьких животных приходится большая площадь поверхности, чем у крупных. Поэтому маленьким животным труднее бороться с холодом³.

 

Бета. Теперь понятно, почему у маленьких синиц перья длиннее ширины тела, а у больших ворон — короче. Синицам нужна шуба теплее — ведь они намного меньше.

 

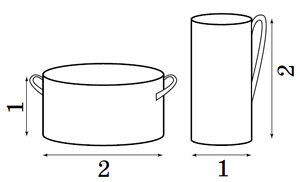
Сигма. А теперь задачи для самостоятельного решения.

1. В какую кастрюлю можно налить больше воды?

 

2. После семи стирок кусок мыла уменьшился вдвое, то есть вдвое уменьшились его длина, ширина и высота. На сколько ещё стирок его хватит?

 

3. Килограмм какой картошки быстрее чистить и почему: мелкой или крупной?

 

4. Великан и лилипут устроили соревнование: кто больше подтянется на перекладине. Кто выиграет и почему?

 

5. По одной гипотезе, гигантские динозавры предпочитали проводить время, стоя в неглубоких водоёмах. Почему?

 

6. Животным пустыни приходится иногда долго не пить. Какое животное может не пить дольше — крупное или мелкое?

 

7. Почему человек ест три раза в день, а, например, хомячки жуют почти постоянно?

И, наконец, два вопроса посложнее:

 

8. Как зависит от размеров животного высота его прыжка?

9. Объясните, почему для мелких дробинок нарушение их правильного расположения вдоль стенок мало влияет на отношение объёмов дробинок и ведра.

 

 

 

 

 

 

Ответы:

1. В левую. При уменьшении высоты объём уменьшается в два раза, а при увеличении диаметра — увеличивается в 22 = 4 раза.

2. На одну. Из 8 маленьких кусочков мыла можно сложить исходный кусок.

3. Крупной. У неё меньше кожуры, потому что если разрезать одну картофелину на несколько мелких, их суммарная площадь поверхности будет больше, чем у исходной картофелины (на удвоенную площадь разрезов).

4. Лилипут. Сила мышц зависит от площади их поперечного сечения, что пропорционально квадрату линейных размеров, а вес — кубу.

5. Например, чтобы спастись от перегрева. В организме постоянно образуется тепло. При большом размере площадь поверхности может быть недостаточной для того, чтобы избавиться от лишнего тепла. Вода же хорошо его отводит. Ещё в воде вес тела меньше и уменьшается нагрузка на кости и мышцы.

6. Крупное, потому что объём запасаемой воды пропорционален кубу линейного размера, а испарение пропорционально площади поверхности. Впрочем, бывают специальные механизмы сохранения воды — например, у тихоходки.

7. Хомячкам, как и человеку, нужно поддерживать высокую температуру тела, но, несмотря на шерсть, тепло они теряют быстро, потому что площадь их поверхности большая по сравнению с их объёмом.

8. Дадим упрощённый ответ (настоящая биомеханика намного сложнее). Мысленно увеличим животное во все стороны в k раз. Как изменится высота его прыжка, когда он прыгает вертикально вверх? Сила мышц пропорциональна площади их поперечного сечения, поэтому она увеличится в k2 раз. Масса увеличится в k2 раз. Значит, ускорение уменьшится в k раз. Казалось бы, высота прыжка уменьшится? Нет, ведь ещё важно, как долго прикладывается это ускорение, то есть пока животное распрямляет ноги и корпус. От этого зависит скорость в момент отрыва, а значит, и высота прыжка. Поскольку животное стало «медлительнее» в k раз, время возрастёт в k раз. И стартовая скорость останется прежней.

Тем самым размер животного лишь косвенно влияет на высоту прыжка. Например, кузнечику сложно преодолевать сопротивление воздуха, и у увеличенной копии есть все шансы прыгнуть выше. У дельфинов высота прыжка определяется предельной скоростью в воде, и про эту скорость сложно сказать, как она зависит от размера: с одной стороны, влияние сопротивления воды уменьшается, а с другой — животное становится менее подвижным.

Не путайте высоту прыжка животного с высотой, на которую оно запрыгивает. Во втором случае животное может помочь себе передними лапами в конце прыжка, и такая высота сильно зависит от размера животного.

9. Будем оптимально заполнять дробинками ведро, пока не дойдём до стенок. У стенок образуется пустота толщиной не больше диаметра дробинки. Объём пустоты очень мал по сравнению с объёмом ведра, если дробинки мелкие.

Источник: «Квант», 1982, № 11